Explora, aprende y diviértete con el
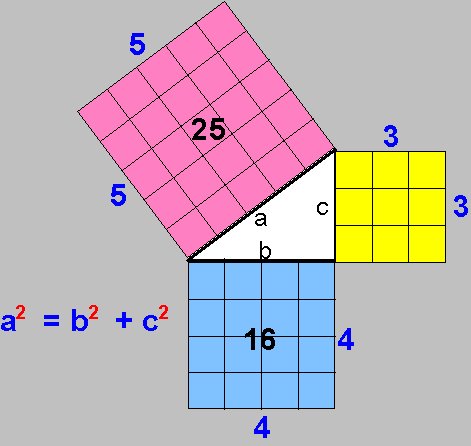
Teorema de Pitágoras
|
Autor: Profa. Thania González E-mail: thania.g05@hotmail.com |
Área: Geometría Nivel: 7º |
|
Pitágoras de Samos
fue un filósofo griego que vivió alrededor del año |
|
|
Realice
las siguientes tareas en grupo de tres integrantes, las cuales se sustentarán
en la última clase: c) Que distancia hay entre “home”
y la segunda base de un diamante de béisbol? Sugerencia: Consulte con su
profesor de educación física la distancia de home a
la primera base y la distancia de la primera base a la segunda. |
|
|
Para poder la tarea es de suma
importancia que antes de iniciar tomemos en cuenta la parte teórica para la
comprensión de conceptos. Para ello, podrás utilizar los links que se
incluyen en el apartado de Recursos; ahí podrás encontrar la información para
comprender las ideas principales. Reflexiona y resume en un mapa mental o
conceptual dicha información, para que construyas tus propios esquemas y los relaciones con la resolución de las tareas. |
|
RECURSOS |
http://youtu.be/k0bG2JuT_Ys |
|
Se evaluará el trabajo grupal
teniendo en cuenta los items que se le proponen. |
|
|
Pitágoras, es el personaje
matemático más famosos, su teorema ha sido una de las herramientas más
utilizadas dentro de la geometría y es útil para calcular ángulos, áreas,
distancias, etc. |
|
|
Esta webquest
fue elaborada por: Thania González |
Imprimir - Arriba
(Página
creada con 1,2,3 Tu WebQuest
- http://www.aula21.net/)




